A few months ago, we made a significant change to our homepage layout on our mobile applications. Specifically, we personalized it across our entire user base so each JioSaavn user could see a homepage that is reflective of their engagement with the content on it. This is a fairly complex problem and in this post we will describe how we attempted to solve this problem.
Recommendation and personalization are central to the JioSaavn user experience. We are constantly striving to present the most relevant content at the right time and place. In this post we will talk about how we leverage contextual bandits to present a personalized homepage experience for our users.
The Problem:
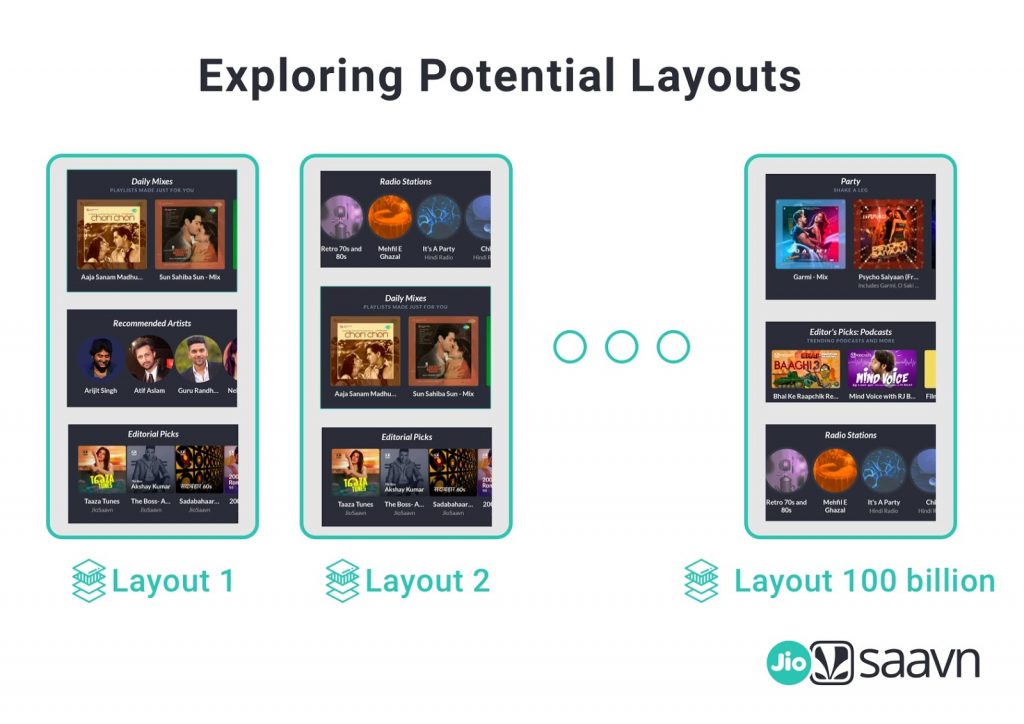
At the time of writing we have over 15 different modules on the homepage ranging from programatically and editorially curated modules such as “new releases”, “top shows”, “editorial picks” etc. to recommendation modules like “recommended artists”, “top picks for you” and a wide range of topics like “Bollywood romantic”, “Party” etc. Consider the problem of re-arranging these modules to reflect the streaming habits of a user. If a user mostly listens to podcasts and new releases then these modules should show up in the first few positions for them.
A/B testing all the variations is not an option because there are an exponentially large number of combinations (nearly 130 billion!) to try. Also, note that user’s interests change over time and the solution must be able to adapt to these changing interests. The broad area of reinforcement learning is well suited to solve this kind of a problem where the algorithm is adaptive to the user’s actions. In particular, we will look at the delightfully named Multi-Armed Bandit and explain how we leverage the solution for the bandit problem for homepage personalization
What is a Multi Armed Bandit?
The Multi Armed Bandit is a gambler’s dilemma. Imagine walking into one of the glitzy casino floors in Vegas where you are presented with a variety of options to spend your money on. You chose the slot machines but now must decide which slot machine to play on. Let us suppose that the odds of payout differ significantly between the various machines. How should you decide which one to play and when to switch to another machine? The slot machine is also known as the one-armed bandit due to its propensity to take your money. If you had an unlimited amount of time and money you could play each slot machine for as long as you like to figure out which has the best expected payout but this is rarely the case in the real world. Hence, we need a way to maximize our earnings while losing as little money as possible (also called incurring minimal “regret” in the world of bandit algorithms). This is the classical multi-armed bandit problem where we must optimize between exploring (searching for the best payout) and exploiting (playing the arm with the expected best payout). Interesting as this problem is, when it was first conceived around World War II, and proved so intractable that allied scientists wanted to drop this problem over Germany so that German scientists could also waste their time on it.
Although we have presented the Multi-armed bandit problem in its original setting, the problem pervades all walks of life where there is a choice between exploring and exploiting. Consider a car purchase as an example. How many cars should you try before you buy one? You spend valuable resources (time and effort) when trying cars and if you decide too soon, you may end up missing out on “better” choices.
Bandits for Personalization
We have established the problem at hand and also outlined the nature of our solution but we have yet not explained how exactly bandits are used to personalize the homepage. Consider each row/module position as an arm of the bandit that presents a module. Each time a user interacts with a specific module (clicks or streams from the module) we consider that a payout was received from that arm. Naturally, modules that have high interaction scores will gain a higher rank on the homepage and modules that do not get interacted with will shift lower.
Note that we are not simply interested in finding the best performing arm/module but the ideal ranking of these modules relative to each other. We must be careful to provide an opportunity to each module to be presented at higher positions to allow for exploration before settling on the ideal ordering. The theoretical basis for this can be found in the work done by radlinski et al in their paper titled:
“Learning Diverse Rankings with Multi-Armed Bandits”
Although the results of their work are independent of the exact bandit algorithm used, let us make these ideas more concrete with an example using a bandit algorithm known as UCB. In UCB, each bandit arm’s score has 2 parts:
- Exploration Score
- Mean reward so far
![]()
Where xj is the mean reward so far and the second part of the formula represents the exploration score for this module. Here t is the total number of impressions across all modules and nj is the number of impressions of the module whose score we are calculating.
Let us consider, as an example the following values for the module “Top Charts”
- 100 impressions for “Top Charts”
- 16 clicks for “Top Charts”
- 4 streams for “Top Charts”
- 1000 total impressions for all modules
And the following values for the module “Daily Mixes”
- 50 impressions for “Daily Mixes”
- 4 clicks for “Daily Mixes”
- 5 streams for “Daily Mixes”
- 1000 total impressions for all modules
Although the interactions(clicks + streams) for “Daily Mixes” is lower, we must consider the fact that a stream is a stronger signal of interest than a click and must be weighted accordingly. We must also take into account the fact that “Daily Mixes” has less impressions than “Top Charts” and should hence be scored higher.
Note some interesting properties about this algorithm. It naturally allows for exploration because modules that do not have many impressions will have a high exploration score and once all modules are sufficiently explored, the mean reward tends to dominate. Another interesting property to note is that it will adapt to changing user tastes. If a user who was previously mostly streaming from the “top charts” modules finds a new interest in “podcasts”, this will naturally be reflected over time as they tend to listen and interact with the “podcasts” module more increasing its mean reward while the mean rewards for “top charts” will diminish.
Making an Impression
While the algorithm described above sounds fairly straightforward, implementing it for a user base of nearly 100 million brings about its own unique engineering challenges. As someone wise once said, “In theory, there is no difference between practice and theory. In practice, there is.”
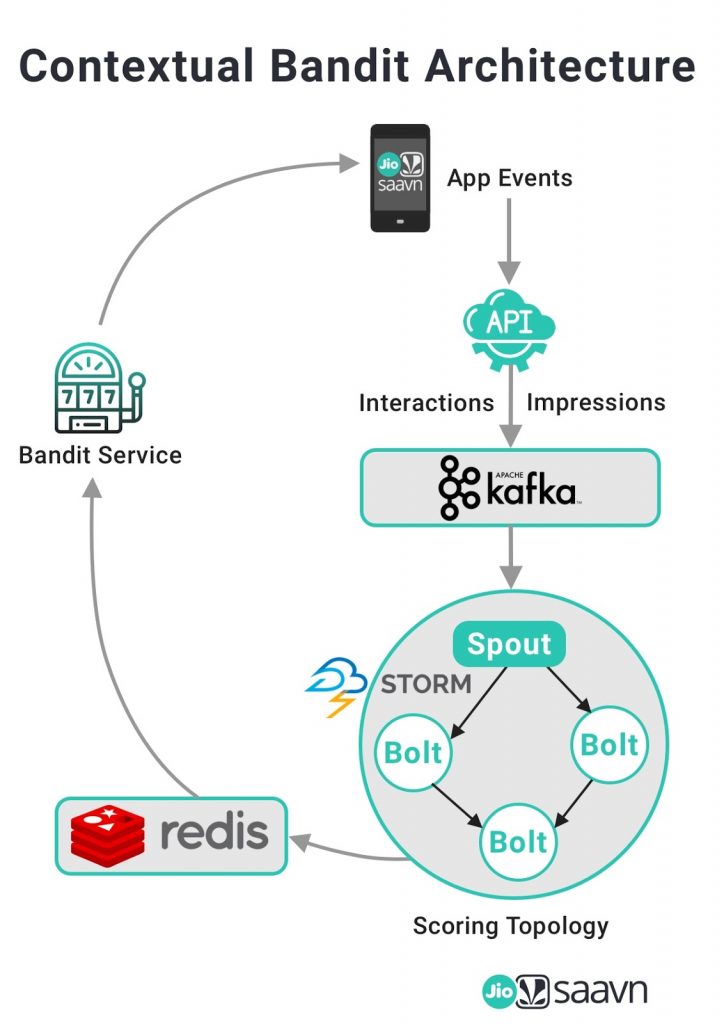
In this section we will describe some of the challenges we faced implementing this solution and how we tackled them. There were a couple of significant obstacles we needed to get over for us to be able to implement a dynamic homepage solution. Firstly, there was a requirement that the homepage should feel “dynamic”. This meant that as the user kept interacting with the modules we wanted to be able to re-arrange them in a near-real time manner. This meant that offline batch processing was not an option. The biggest challenge however, was being able to capture impressions for all modules at this scale and scoring them in near real time. Enter – ace ninjaneer Mahendra singh meena and wizard of all things data – Srijan Patel. Together they were able to figure out a way to capture impression data from our logs and capture relevant events that could be streamed through a storm topology and stored in redis. The backend layer would capture all relevant impressions and interactions and write to the appropriate kafka topic where they are consumed by a storm topology which assigns impression and interaction scores and stores it in redis on a per user basis.
At every homepage reload event, the scores would get updated in redis thus also addressing the near-real time requirement. Given the scale of our operation, this was a remarkable feat of engineering which went from conceptualization to production in a matter of a few weeks. Once this data was present in redis we were able to implement the algorithm in our backend layer by simply reading the scores from redis for each user and sorting the modules according to the score.
How did we fare?
With all the necessary infrastructure in place, we set out experimenting the dynamic homepage on 5% of our user base. We started with an epsilon-greedy variant of the bandit algorithm as it was the simplest to implement. The results were highly encouraging and it moved all the key metrics we were looking at in the right direction. Although we are unable to share fine grained metrics suffice to note that perhaps the most important measure – user engagement – which is well represented by the average listening time per user went up by 7%. We have since rolled out this feature to our entire user base and continue to experiment with our scoring and algorithms to further refine our personalization strategies.
References:
https://medium.com/scribd-data-science-engineering/multi-armed-bandits-for-the-win-240b71bc3464
https://www.cs.cornell.edu/people/tj/publications/radlinski_etal_08a.pdf
https://jeremykun.com/2013/10/28/optimism-in-the-face-of-uncertainty-the-ucb1-algorithm/
